MA.3.1 导数
导数
导数的定义
-
切线
-
速度
几何、物理意义

单侧导数
左导数略
证明
证明:
Example
Corollary
Example
导函数
Definition
导数公式
给出一些证明如下:
可导一定连续
Corollary
可以理解为:
证明:
连续未必可导
左可导=>左连续; 右可导=>右连续
左右可导且相等=>可导
左可导右可导未必可导; 左可导右可导一定连续
Example
切线为
导数的线性运算
Theorem
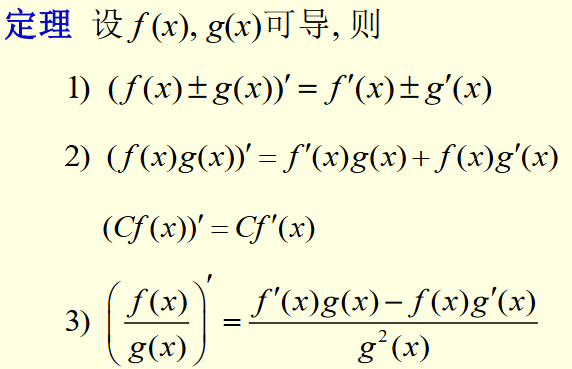
复合函数导数
反映了复合过程:
Example
证明:
推广到一般形式:
幂指函数的导数
Example
(1). 复合函数求导 (2). 对数求导法
反函数的导数
Example
基本导数表
基本导数表
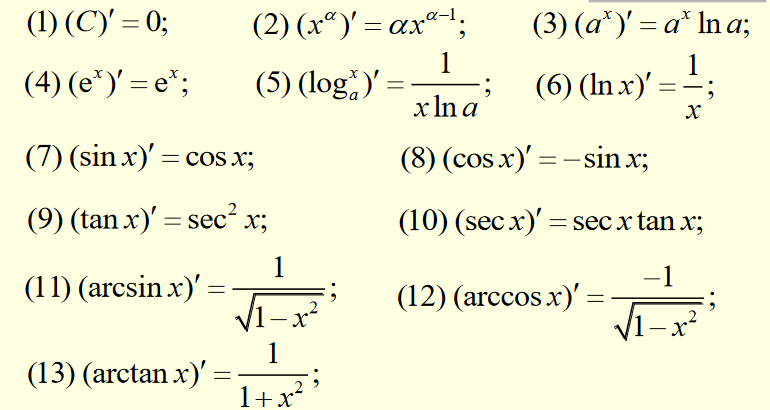
高阶导数
Definition
二阶导的前提: 在该点邻域内有一阶导

Example
多项式的高阶导
Example

- 三角函数: 导数增加
相位 - L13:
类二项式定理, 证明使用数学归纳法
Example
证明:
参数方程表示的函数的导数
向量函数的导数


